Pythonでボールねじとモーターとカップリングの選定をしてみる 全通り計算編

2020/03/14 categories:NX Journal| tags:Python|Ballscrew|NumPy|Python|Mechanical design|

ボールねじを使用した直動機構で、ボールねじとモーターとカップリングの選定をPythonで行ってみました。選定といっても、固定-支持の構成で全通り計算をPythonで行うという内容です。計算内容はメーカーカタログなどを参考にしています。

なぜ全通り計算をするのか

部品メーカーではHP上で計算ツールを公開しているのでそのツールを利用すれば簡単に計算できるのですが、部品メーカーもたくさんあるので色々なメーカーでどれが良さそうか検討する場合には、いろんなメーカーのツールを使用してそれぞれ計算する必要があり、地味にめんどくさいです。

そこでボールねじリスト、モーターリスト、カップリングリストの3つのリストを用意して、それらのリストを全通り計算して条件を満たす組み合わせを検索すると設計が楽になりそうです。エクセルのマクロで組み合わせの計算をしてもいいのですが、VBAが嫌いという理由と、PythonのNumPyの方が計算速度が速そうという理由でPythonで計算をしてみました。

ボールねじリスト

各社メーカーのカタログから計算に必要なパラメータを下記のようなCSVとして用意しました。

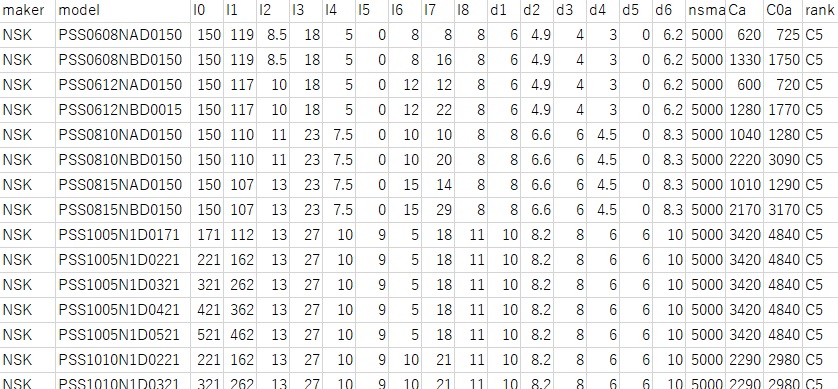
nsmaxは固定-支持の時のDN値による許容回転数、Caは動定格荷重、C0aは静定格荷重、rankは等級、l0～d6までの値は下記の通りです。

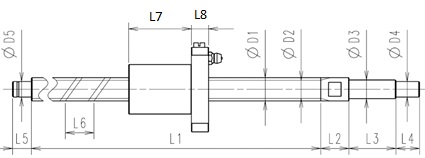
モーターリスト

下記のようなCSVです。

カップリングリスト

下記のようなCSVです。

ボールねじに関する計算

ボールねじメーカーのカタログを参考にして、下記のような関数で計算しています。

def ballscrew_calculate(m, n, fs, Fa, fw, f, l, d, Ca, C0a):
    '''
    m  : 座屈荷重係数 19.9, 10.0, 1.2, 5.0
    n  : 回転数 [rpm]
    fs : 静許容荷重係数 1.0~2.0, 1.5~3.0
    Fa : 軸方向荷重 [N]
    fw : 荷重係数 1.0~1.2, 1.2~1.5, 1.5~3.0
    f  : 危険速度係数 21.9, 15.1, 9.7, 3.4
    l  : ボールねじ長さリスト [mm]
    d  : ボールねじ径リスト [mm]
    Ca : 動定格荷重 [N]
    C0a: 静定格荷重 [N]
    '''
    P1 = m * np.power(d[1], 4.0) / ( l[3] / 2.0 + l[2] + l[1] - l[7] / 2.0 ) # 座屈荷重
    P2 = 115.45353 * np.power(d[1], 2.0) # 降伏荷重
    P0 = C0a / fs # 静最大許容荷重
    nc = f * np.power(d[1], 2.0) *(10.0**7.0) / ( l[5] + l[1] - l[8] - l[7]/2.0 ) # 危険速度
    L  = np.power( ( Ca/(Fa*fw) ) , 3.0) * (10.0**6.0) # 寿命回転数
    Lt = L / 60.0 / n # 寿命時間
    Ls = L * l[6] * (10.0**(-6.0)) # 寿命距離
    return(P1,P2,P0,nc,L,Lt,Ls)

引数はすべてNumPy配列を想定しています。NumPy配列のべき乗はnp.powerを使わなければいけませんが、それ以外は単純な四則演算です。

モーターの計算

モーターメーカーのカタログを参考に下記のような関数で計算します。変数はすべてNumPy配列です。

def motor_calculate(m, n, l, d, Ic, Im):
    '''
    m : ワーク質量[kg]
    n : 回転数[rpm]
    l  : ボールねじ長さリスト [mm]
    d  : ボールねじ径リスト [mm]
    Ic : カップリングイナーシャ[kg*m**2]
    Im : モーターイナーシャ[kg*m**2]
    '''
    a  = 2.0 * math.pi * n * 1000.0 / l[6] # 角加速度
    Iw = m * ( l[6]*10.0**(-3.0) / (2.0*math.pi) )**2.0 # ワークのイナーシャ
    Is = math.pi * 0.24375 * l[0] * d[0]**4.0 * 10.0**(-12.0) # ボールねじ軸のイナーシャ [kg*m**2]
    Ir = ( Is + Iw + Ic ) / Im # イナーシャ比
    t  = ( Is + Iw + Ic + Im ) * a # トルク
    return (a,Iw,Is,Ir,t)

安全率の計算

それぞれの許容値を計算値で割った値を安全率として、下記の関数で計算しています。変数はすべてNumPy配列です。

def calculate_safety_factor(P0,P1,P2,Fa,n,nc,mt,Ir,t):
    '''
    P0 : 静的最大許容荷重[N]
    P1 : 座屈荷重[N]
    P2 : 降伏荷重[N]
    Fa : 軸方向荷重[N]
    n  : 回転数[rpm]
    nc : 危険速度[rpm]
    mt : モーターの最大トルク[Nm]
    Ir : イナーシャ比
    t  : 駆動トルク[Nm]
    '''
    sf_static_load = P0 / Fa # 静最大許容荷重
    sf_buckl_load  = P1 / Fa # 座屈荷重
    sf_yield_load  = P2 / Fa # 降伏荷重
    sf_critical_speed = nc / n # 危険速度
    sf_ir = mt[5] / Ir # イナーシャ比
    sf_t = mt[3] / t # トルク
    return (sf_static_load, sf_buckl_load, sf_yield_load, sf_critical_speed, sf_ir, sf_t)

リストの読み込み

pandasのread_csvで3つのリストを読み込みます。

bs = pd.read_csv('ballscrew2.csv',  encoding='utf-8')
cp = pd.read_csv('coupling2.csv',  encoding='utf-8')
mt = pd.read_csv('motor2.csv',  encoding='utf-8')

組み合わせの作成

itertoolsのproductで3つのリストの組み合わせを全通り列挙します。

import itertools
ls = list( itertools.product(bs.values, cp.values, mt.values) )

配列の変形

配列の形を扱いやすい形に変形するためにNumPy配列の転置Tで形を変えます。

bs = np.array([ row[0].T for row in ls ]).T
cp = np.array([ row[1].T for row in ls ]).T
mt = np.array([ row[2].T for row in ls ]).T

設計値の配列作成

NumPy配列を使って配列同士の計算を一気に行うので、ボールねじリストの配列と同じサイズで設計値の配列を作成します。

cnt = len(bs[0])
m = np.full(cnt, 19.9)  # 座屈荷重係数 19.9, 10.0, 1.2, 5.0
n = np.full(cnt, 2000.0)  # 回転数 [rpm]
fs = np.full(cnt, 2.0) # 静許容荷重係数 1.0~2.0, 1.5~3.0
Fa = np.full(cnt, 50.0) # 軸方向荷重 [N]
fw = np.full(cnt, 1.5) # 荷重係数 1.0~1.2, 1.2~1.5, 1.5~3.0
f = np.full(cnt, 15.1)  # 危険速度係数 21.9, 15.1, 9.7, 3.4
mw = np.full(cnt, 20.0) # ワーク質量[kg]
l = np.array([ np.full(cnt, bs[i+2]) for i in range(9) ])
d = np.array([ np.full(cnt, bs[i+11]) for i in range(6) ])

計算の実行

先ほどの関数を呼び出して計算します。

## ボールねじ計算
(P1,P2,P0,nc,L,Lt,Ls) = ballscrew_calculate(m, n, fs, Fa, fw, f, l, d, bs[18], bs[19])
## モーター計算
(a,Iw,Is,Ir,t) = motor_calculate(mw, n, l, d, cp[11], mt[4])
## 安全率計算
(sf_sl, sf_bl, sf_yl, sf_cs, sf_ir, sf_t) = calculate_safety_factor(P0,P1,P2,Fa,n,nc,mt,Ir,t)

結果をCSVで保存

すべての結果の配列をextendで配列の下方向に結合していきます。結合後の配列は配列の横方向に組み合わせが並んでいる状態ですので、NumPy配列の転置Tで組み合わせが下方向に並ぶように転置します。その配列をpandasのDataFrameに変換した後、CSVとして出力します。

## 保存
stack_list = [ i for i in bs ]
stack_list.extend([ i for i in cp ])
stack_list.extend([ i for i in mt ])
stack_list.extend([
    m,n,fs,Fa,fw,f,mw,P1,P2,P0,nc,L,Lt,Ls,a,
    Iw,Is,Ir,t,sf_sl, sf_bl, sf_yl, sf_cs, sf_ir, sf_t
])
columns = ["bs_maker","bs_model","bs_l0","bs_l1","bs_l2","bs_l3","bs_l4","bs_l5","bs_l6","bs_l7","bs_l8",
"bs_d0","bs_d1","bs_d2","bs_d3","bs_d4","bs_d5","bs_nsmax","bs_Ca","bs_C0a","bs_rank","cp_maker","cp_model",
"cp_l0","cp_d0","cp_d1","cp_d2","cp_t0","cp_t1","cp_nmax","cp_k","cp_m","cp_i","mt_maker","mt_model","mt_p",
"mt_t0","mt_i","mt_ir","mt_l0","mt_nmax","mt_nnor","mt_v","mt_d0","m","n","fs","Fa","fw","f","mw","P1","P2",
"P0","nc","L","Lt","Ls","a","Iw","Is","Ir","t","sf_sl","sf_bl","sf_yl","sf_cs","sf_ir","sf_t"]
df = pd.DataFrame(np.array(stack_list).T, columns=columns)
df.to_csv("output.csv")

所感

このコードで計算を行ってメーカーと型式を選んだ後、メーカーのツールで計算を確認するという流れで部品選定をすると結構楽になりました。また、計算結果から色々な比較ができて結構便利です。

計算に使ったリストはボールねじ47通り、カップリング9通り、モーター42通りで、処理時間は0.96秒で、メモリは51MBくらい消費していました。

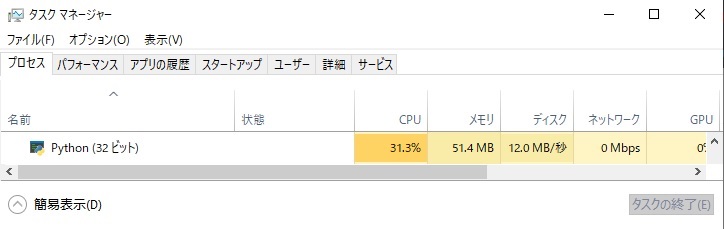
ボールねじを1155通りに増やして計算したところ23.69秒で、メモリは482MBくらい消費していました。

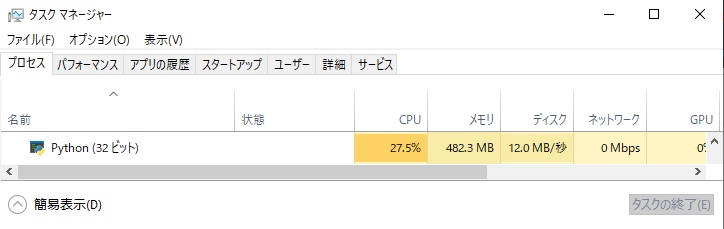
ちなみにボールねじ1155通りの計算結果のCSVファイルは255MBにもなって、エクセルで開くのに1分以上かかったので、Python上で条件を絞る処理を追加して不要なデータは出力しないように改良したいと思います。

そのほかにも、カップリングの計算の追加やGUIの追加などいろいろ改良したいと思います。

ソースコード

## -*- coding: utf-8 -*-
import csv
import itertools
import math
import numpy as np
import pandas as pd
def ballscrew_calculate(m, n, fs, Fa, fw, f, l, d, Ca, C0a):
    '''
    m  : 座屈荷重係数 19.9, 10.0, 1.2, 5.0
    n  : 回転数 [rpm]
    fs : 静許容荷重係数 1.0~2.0, 1.5~3.0
    Fa : 軸方向荷重 [N]
    fw : 荷重係数 1.0~1.2, 1.2~1.5, 1.5~3.0
    f  : 危険速度係数 21.9, 15.1, 9.7, 3.4
    l  : ボールねじ長さリスト [mm]
    d  : ボールねじ径リスト [mm]
    Ca : 動定格荷重 [N]
    C0a: 静定格荷重 [N]
    '''
    P1 = m * np.power(d[1], 4.0) / ( l[3] / 2.0 + l[2] + l[1] - l[7] / 2.0 ) # 座屈荷重
    P2 = 115.45353 * np.power(d[1], 2.0) # 降伏荷重
    P0 = C0a / fs # 静最大許容荷重
    nc = f * np.power(d[1], 2.0) *(10.0**7.0) / ( l[5] + l[1] - l[8] - l[7]/2.0 ) # 危険速度
    L  = np.power( ( Ca/(Fa*fw) ) , 3.0) * (10.0**6.0) # 寿命回転数
    Lt = L / 60.0 / n # 寿命時間
    Ls = L * l[6] * (10**(-6)) # 寿命距離
    return(P1,P2,P0,nc,L,Lt,Ls)
def motor_calculate(m, n, l, d, Ic, Im):
    '''
    m : ワーク質量[kg]
    n : 回転数[rpm]
    l  : ボールねじ長さリスト [mm]
    d  : ボールねじ径リスト [mm]
    Ic : カップリングイナーシャ[kg*m**2]
    Im : モーターイナーシャ[kg*m**2]
    '''
    a  = 2.0 * math.pi * n * 1000.0 / l[6] # 角加速度
    Iw = m * ( l[6]*10.0**(-3.0) / (2.0*math.pi) )**2.0 # ワークのイナーシャ
    Is = math.pi * 0.24375 * l[0] * d[0]**4.0 * 10.0**(-12.0) # ボールねじ軸のイナーシャ [kg*m**2]
    Ir = ( Is + Iw + Ic ) / Im # イナーシャ比 = モーター以外のイナーシャ合計 / モーターのイナーシャ
    t  = ( Is + Iw + Ic + Im ) * a # トルク = イナーシャ合計 * 角加速度
    return (a,Iw,Is,Ir,t)
def calculate_safety_factor(P0,P1,P2,Fa,n,nc,mt,Ir,t):
    '''
    P0 : 静的最大許容荷重[N]
    P1 : 座屈荷重[N]
    P2 : 降伏荷重[N]
    Fa : 軸方向荷重[N]
    n  : 回転数[rpm]
    nc : 危険速度[rpm]
    mt : モーターの最大トルク[Nm]
    Ir : イナーシャ比
    t  : 駆動トルク[Nm]
    '''
    sf_static_load = P0 / Fa # 静最大許容荷重
    sf_buckl_load  = P1 / Fa # 座屈荷重
    sf_yield_load  = P2 / Fa # 降伏荷重
    sf_critical_speed = nc / n # 危険速度
    sf_ir = mt[5] / Ir # イナーシャ比
    sf_t = mt[3] / t # トルク
    return (sf_static_load, sf_buckl_load, sf_yield_load, sf_critical_speed, sf_ir, sf_t)
def main():
    bs = pd.read_csv('ballscrew2.csv',  encoding='utf-8')
    cp = pd.read_csv('coupling2.csv',  encoding='utf-8')
    mt = pd.read_csv('motor2.csv',  encoding='utf-8')
    
    ls = list( itertools.product(bs.values, cp.values, mt.values) )
    
    bs = np.array([ row[0].T for row in ls ]).T
    cp = np.array([ row[1].T for row in ls ]).T
    mt = np.array([ row[2].T for row in ls ]).T
    
    cnt = len(bs[0])
    m = np.full(cnt, 19.9)  # 座屈荷重係数 19.9, 10.0, 1.2, 5.0
    n = np.full(cnt, 2000.0)  # 回転数 [rpm]
    fs = np.full(cnt, 2.0) # 静許容荷重係数 1.0~2.0, 1.5~3.0
    Fa = np.full(cnt, 50.0) # 軸方向荷重 [N]
    fw = np.full(cnt, 1.5) # 荷重係数 1.0~1.2, 1.2~1.5, 1.5~3.0
    f = np.full(cnt, 15.1)  # 危険速度係数 21.9, 15.1, 9.7, 3.4
    mw = np.full(cnt, 20.0) # ワーク質量[kg]
    l = np.array([ np.full(cnt, bs[i+2]) for i in range(9) ])
    d = np.array([ np.full(cnt, bs[i+11]) for i in range(6) ])
    
    # ボールねじ計算
    (P1,P2,P0,nc,L,Lt,Ls) = ballscrew_calculate(m, n, fs, Fa, fw, f, l, d, bs[18], bs[19])
    
    # モーター計算
    (a,Iw,Is,Ir,t) = motor_calculate(mw, n, l, d, cp[11], mt[4])
    # 安全率計算
    (sf_sl, sf_bl, sf_yl, sf_cs, sf_ir, sf_t) = calculate_safety_factor(P0,P1,P2,Fa,n,nc,mt,Ir,t)
    
    # 保存
    stack_list = [ i for i in bs ]
    stack_list.extend([ i for i in cp ])
    stack_list.extend([ i for i in mt ])
    stack_list.extend([
        m,n,fs,Fa,fw,f,mw,P1,P2,P0,nc,L,Lt,Ls,a,
        Iw,Is,Ir,t,sf_sl, sf_bl, sf_yl, sf_cs, sf_ir, sf_t
    ])
    columns = ["bs_maker","bs_model","bs_l0","bs_l1","bs_l2","bs_l3","bs_l4","bs_l5","bs_l6","bs_l7","bs_l8",
    "bs_d0","bs_d1","bs_d2","bs_d3","bs_d4","bs_d5","bs_nsmax","bs_Ca","bs_C0a","bs_rank","cp_maker","cp_model",
    "cp_l0","cp_d0","cp_d1","cp_d2","cp_t0","cp_t1","cp_nmax","cp_k","cp_m","cp_i","mt_maker","mt_model","mt_p",
    "mt_t0","mt_i","mt_ir","mt_l0","mt_nmax","mt_nnor","mt_v","mt_d0","m","n","fs","Fa","fw","f","mw","P1","P2",
    "P0","nc","L","Lt","Ls","a","Iw","Is","Ir","t","sf_sl","sf_bl","sf_yl","sf_cs","sf_ir","sf_t"]
    df = pd.DataFrame(np.array(stack_list).T, columns=columns)
    df.to_csv("output.csv")
if __name__ == '__main__':
    main()

Share post

Related Posts

Pythonで作るシンプル画像ビューワ

PyQt5 QTableViewのサンプル

Pythonで圧縮コイルバネの計算をしてみる

PyQt5 Qt DesignerでGUIをフラットっぽくしてみる

Pythonで圧縮コイルバネの計算をしてみる NumPy版

Pythonで作るn次元n目並べ その2:1次元n目並べ速度計測

Pythonで作るn次元n目並べ その1:1次元n目並べ

Pythonで作る大量のPDFに一括で押印するツール

コメント