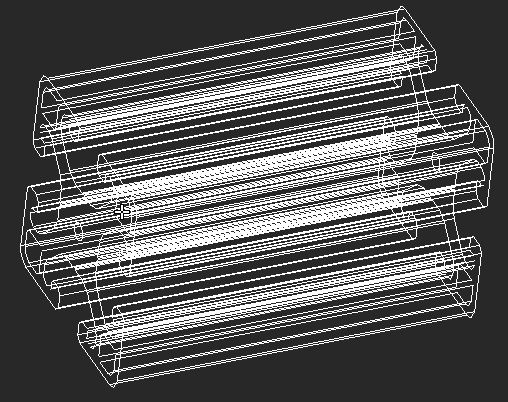
iCAD SXのボディを点群に変換

2024/04/07 categories:iCAD SX| tags:iCAD SX|Python|

iCAD SXの3D上のボディに含まれるエッジを点群として作成するプログラムを作ってみました。

パーツの選択

点群に変換する対象パーツを選択するようにしました。選択せずにGOするとトップパーツの要素を処理します。

def main():
    wf = sxnet.SxWF.getActive()
    if wf is None:
        return
    
    entparts = sxnet.SxSys.getEntList(sxnet.SxSys.ENTMODE_PART)

    if entparts is None:
        part_to_points(wf, None)
    else:
        for entpart in entparts:
            part_to_points(wf, entpart)

    sxnet.SxEntPart.setActiveTop()

ボディからエッジを取得

パーツに含まれるボディからエッジを取得して、そのエッジのジオメトリから点の座標を計算します。

    if entpart is None:
        seglist = wf.getTopSegList(offset=0, num=0, visi=True, layer=True, type=True)
    else:
        seglist = entpart.getEntList()
    
    bodies, _body_types = [], body_types()
    for seg in seglist:
        if seg.Type in _body_types:
            bodies.append(seg)
    
    edges = sxnet.SxEntSeg.getEdgeList(bodies)
    if edges is None:
        return
    
    edges = sum([ list(edges2) for edges2 in edges ], [])
    geoms = sxnet.SxEdge.getGeomList(edges)
    
    lines, circles, arcs = [], [], []
    for geom in geoms:
        if geom.type == sxnet.SxGeom.TYPE_LINE3D:
            lines.append(geom)
        elif geom.type == sxnet.SxGeom.TYPE_CIRCLE3D:
            circles.append(geom)
        elif geom.type == sxnet.SxGeom.TYPE_ARC3D:
            arcs.append(geom)

ジオメトリから点を作成

ジオメトリのタイプごとに点を作成する関数を作って、線はline_pointsで、円はcircle_points、円弧はarc_pointsで点を計算しています。

    points = []

    for line in lines:
        count = int(line.leng/20) + 3
        created_line = line_points(line, count)
        points.append(created_line)

    for circle in circles:
        created_circle = circle_points(circle, 4)
        points.append(created_circle)

    for arc in arcs:
        created_arc = arc_points(arc, 4)
        points.append(created_arc)

線のジオメトリから線上の点の座標を計算

線のジオメトリからは、始点とベクトル、長さの情報があるので、それらの値を使って線上の点の座標を計算します。終点を計算する場合は、始点×ベクトル×長さで計算できます。始点と終点の間の点の座標を計算をする場合は、長さに対して1未満の値を掛けると計算できます。間の点は基本的に3個計算して、長さ20mm毎に1個増やすようにしています。

        count = int(line.leng/20) + 3
        created_line = line_points(line, count)

def line_points(geom, count):
    v = (geom.vec.x * geom.leng, geom.vec.y * geom.leng, geom.vec.z * geom.leng)
    points = []
    for i in range(count):
        a = i / (count - 1)
        p = sxnet.SxPos(geom.sp.x + v[0] * a, geom.sp.y + v[1] * a, geom.sp.z + v[2] * a)
        points.append(p)
    return points

円弧上の点の座標を計算

_arc_pointsに円弧の中心座標(center)、半径(radius)、円弧の方向のベクトル(axis)、円弧の始点がある方向のベクトル(v1)、円弧の終点がある方向のベクトル(v2)、計算する点の個数(count)を渡して、円弧上の点の座標の計算しています。

まずはnumpy.arccosでv1とv2のなす角の角度(total_angle)を計算して、total_angleをcountの分だけ分割したangleを計算します。このangleの角度分だけ、v1をaxisの周りに回転したベクトルrotatedを計算します。ベクトルrotatedの方向にある円弧上の点の座標はcenter + rotated * radiusで計算できます。

def _arc_points(center, radius, axis, v1, v2, count):
    total_angle = numpy.arccos( numpy.dot(v1, v2) / ( numpy.linalg.norm(v1) * numpy.linalg.norm(v2) ) )
    points = []
    for i in range(count):
        angle = total_angle * i / (count - 1)
        rotated = rotate_vector(v1, axis, angle)
        p = center + rotated * radius
        points.append(sxnet.SxPos(p[0], p[1], p[2]))
    return points

ベクトルをほかのベクトル周りに回転させたベクトルを計算するには、回転軸のベクトルから回転行列の係数matを計算します。その係数のcosの値cos_thetaと、sinの値sin_thetaを計算して、それらの値で回転行列を計算します。そして、回転するベクトルと回転行列を計算すると、回転後のベクトルが計算できます。

def rotate_vector(v, axis, angle):
    axis = axis / numpy.linalg.norm(axis)
    mat = numpy.array([
        [       0, -axis[2],  axis[1]],
        [ axis[2],        0, -axis[0]],
        [-axis[1],  axis[0],        0]
    ])
    cos_theta = numpy.cos(angle)
    sin_theta = numpy.sin(angle)
    rot_matrix = cos_theta * numpy.eye(3) + (1 - cos_theta) * numpy.outer(axis, axis) + sin_theta * mat
    return numpy.dot(rot_matrix, v)

円弧のジオメトリから円弧上の点を計算

円弧上の点を計算する関数に円弧のジオメトリの値を渡して計算しています。

def arc_points(geom, count):
    axis   = numpy.array([geom.axis.x, geom.axis.y, geom.axis.z])
    v1     = numpy.array([geom.vecs.x, geom.vecs.y, geom.vecs.z])
    v2     = numpy.array([geom.vece.x, geom.vece.y, geom.vece.z])
    center = numpy.array([  geom.cp.x,   geom.cp.y,   geom.cp.z])
    points = _arc_points(center, geom.radius, axis, v1, v2, count)
    return points

円のジオメトリから円上の点を計算

円は4つの90度の円弧として扱い、それらの円弧の円弧上の点を計算しています。円弧の各ベクトルは以下のように計算しています。

円の回転軸axisと直行するベクトルv1を計算(axisと[1, 0, 0]の外積をv1として、v1が0なら[0, 1, 0]との外積をv1とする)
axisとv1に直行するベクトルv2を計算(axisとv1の外積)
axisとv2に直行するベクトルv3を計算(axisとv2の外積)
axisとv3に直行するベクトルv4を計算(axisとv3の外積)
axisとv3に直行するベクトルv3を計算(axisとv4の外積)

これらのベクトルから、1つめの円弧はv1からv2までの円弧、2つめの円弧はv2からv3までの円弧というように円弧を求められます。この円弧上の点を計算して、円上の点としています。

def circle_points(geom, count):
    axis   = numpy.array([geom.axis.x, geom.axis.y, geom.axis.z])

    v1 = numpy.cross(axis, [1, 0, 0])
    if numpy.allclose(v1, 0):
        v1 = numpy.cross(axis, [0, 1, 0])
    v1 = v1 / numpy.linalg.norm(v1)
    v2 = numpy.cross(axis, v1)
    v3 = numpy.cross(axis, v2)
    v4 = numpy.cross(axis, v3)
    v5 = numpy.cross(axis, v4)

    center = numpy.array([  geom.cp.x,   geom.cp.y,   geom.cp.z])
    points  = _arc_points(center, geom.radius, axis, v1, v2, count)
    points += _arc_points(center, geom.radius, axis, v2, v3, count)
    points += _arc_points(center, geom.radius, axis, v3, v4, count)
    points += _arc_points(center, geom.radius, axis, v4, v5, count)
    return points

実行の様子

プログラムを実行すると、ボディから点を作成して、パーツに入れます。

実行ファイル

body_to_points.exeを実行すると処理できます。

body_to_points.exeをダウンロード

Pythonコード

import clr
import os
import numpy
clr.AddReference( os.getenv('ICADDIR') + '\\bin\\sxnet.dll' )
import sxnet


def main():
    wf = sxnet.SxWF.getActive()
    if wf is None:
        return
    
    entparts = sxnet.SxSys.getEntList(sxnet.SxSys.ENTMODE_PART)

    if entparts is None:
        part_to_points(wf, None)
    else:
        for entpart in entparts:
            part_to_points(wf, entpart)

    sxnet.SxEntPart.setActiveTop()


def part_to_points(wf, entpart):

    if entpart is None:
        seglist = wf.getTopSegList(offset=0, num=0, visi=True, layer=True, type=True)
    else:
        seglist = entpart.getEntList()
    
    bodies, _body_types = [], body_types()
    for seg in seglist:
        if seg.Type in _body_types:
            bodies.append(seg)
    
    edges = sxnet.SxEntSeg.getEdgeList(bodies)
    if edges is None:
        return
    
    edges = sum([ list(edges2) for edges2 in edges ], [])
    geoms = sxnet.SxEdge.getGeomList(edges)
    
    lines, circles, arcs = [], [], []
    for geom in geoms:
        if geom.type == sxnet.SxGeom.TYPE_LINE3D:
            lines.append(geom)
        elif geom.type == sxnet.SxGeom.TYPE_CIRCLE3D:
            circles.append(geom)
        elif geom.type == sxnet.SxGeom.TYPE_ARC3D:
            arcs.append(geom)
    
    points = []

    for line in lines:
        count = int(line.leng/20) + 3
        created_line = line_points(line, count)
        points.append(created_line)

    for circle in circles:
        created_circle = circle_points(circle, 4)
        points.append(created_circle)

    for arc in arcs:
        created_arc = arc_points(arc, 4)
        points.append(created_arc)

    if len(points) == 0:
        return
    
    created = []
    points = sum([ list(points2) for points2 in points if points2 is not None ], [])
    for point in points:
        point = sxnet.SxEntSeg.createPoint3D(point)
        created.append(point)

    if entpart is None:
        sxnet.SxEntPart.setActiveTop()
        sxnet.SxEntPart.create(created, '点群', '', 1)
    else:
        entpart.setActive(False)
        created_part = entpart.create('点群')
        created_part.add(created)


def line_points(geom, count):
    v = (geom.vec.x * geom.leng, geom.vec.y * geom.leng, geom.vec.z * geom.leng)
    points = []
    for i in range(count):
        a = i / (count - 1)
        p = sxnet.SxPos(geom.sp.x + v[0] * a, geom.sp.y + v[1] * a, geom.sp.z + v[2] * a)
        points.append(p)
    return points


def circle_points(geom, count):
    axis   = numpy.array([geom.axis.x, geom.axis.y, geom.axis.z])

    v1 = numpy.cross(axis, [1, 0, 0])
    if numpy.allclose(v1, 0):
        v1 = numpy.cross(axis, [0, 1, 0])
    v1 = v1 / numpy.linalg.norm(v1)
    v2 = numpy.cross(axis, v1)
    v3 = numpy.cross(axis, v2)
    v4 = numpy.cross(axis, v3)
    v5 = numpy.cross(axis, v4)

    center = numpy.array([  geom.cp.x,   geom.cp.y,   geom.cp.z])
    points  = _arc_points(center, geom.radius, axis, v1, v2, count)
    points += _arc_points(center, geom.radius, axis, v2, v3, count)
    points += _arc_points(center, geom.radius, axis, v3, v4, count)
    points += _arc_points(center, geom.radius, axis, v4, v5, count)
    return points


def arc_points(geom, count):
    axis   = numpy.array([geom.axis.x, geom.axis.y, geom.axis.z])
    v1     = numpy.array([geom.vecs.x, geom.vecs.y, geom.vecs.z])
    v2     = numpy.array([geom.vece.x, geom.vece.y, geom.vece.z])
    center = numpy.array([  geom.cp.x,   geom.cp.y,   geom.cp.z])
    points = _arc_points(center, geom.radius, axis, v1, v2, count)
    return points


def _arc_points(center, radius, axis, v1, v2, count):
    total_angle = numpy.arccos( numpy.dot(v1, v2) / ( numpy.linalg.norm(v1) * numpy.linalg.norm(v2) ) )
    points = []
    for i in range(count):
        angle = total_angle * i / (count - 1)
        rotated = rotate_vector(v1, axis, angle)
        p = center + rotated * radius
        points.append(sxnet.SxPos(p[0], p[1], p[2]))
    return points


def rotate_vector(v, axis, angle):
    axis = axis / numpy.linalg.norm(axis)
    mat = numpy.array([
        [       0, -axis[2],  axis[1]],
        [ axis[2],        0, -axis[0]],
        [-axis[1],  axis[0],        0]
    ])
    cos_theta = numpy.cos(angle)
    sin_theta = numpy.sin(angle)
    rot_matrix = cos_theta * numpy.eye(3) + (1 - cos_theta) * numpy.outer(axis, axis) + sin_theta * mat
    return numpy.dot(rot_matrix, v)


def body_types():
    return [
        sxnet.SxEntSeg.SEGTYPE_BOX,     # 直方体  
        sxnet.SxEntSeg.SEGTYPE_CAP,     # キャップ  
        sxnet.SxEntSeg.SEGTYPE_CONE,    # 円錐／円錐台  
        sxnet.SxEntSeg.SEGTYPE_CYL,     # 円柱  
        sxnet.SxEntSeg.SEGTYPE_EPRJ,    # 拡張投影体  
        sxnet.SxEntSeg.SEGTYPE_FCSOLID, # F.C.ソリッド  
        sxnet.SxEntSeg.SEGTYPE_LPRJ,    # 偏心投影体  
        sxnet.SxEntSeg.SEGTYPE_PCON,    # 正多角錐／正多角錐台  
        sxnet.SxEntSeg.SEGTYPE_PCYL,    # 正多角柱  
        sxnet.SxEntSeg.SEGTYPE_PRJT,    # 投影体  
        sxnet.SxEntSeg.SEGTYPE_PRSM,    # 多角錐／多角錐台  
        sxnet.SxEntSeg.SEGTYPE_ROT,     # 回転体  
        sxnet.SxEntSeg.SEGTYPE_SOLID,   # ソリッド  
        sxnet.SxEntSeg.SEGTYPE_SPHR,    # 球／部分球  
        sxnet.SxEntSeg.SEGTYPE_TORUS    # トーラス  
    ]


if __name__ == '__main__':
    main()