Pythonで作るモーター駆動パターングラフ作成ツールにS字駆動追加

以前作成したモーター駆動パターンのグラフ作成ツールにS字駆動の描画機能を追加しました。

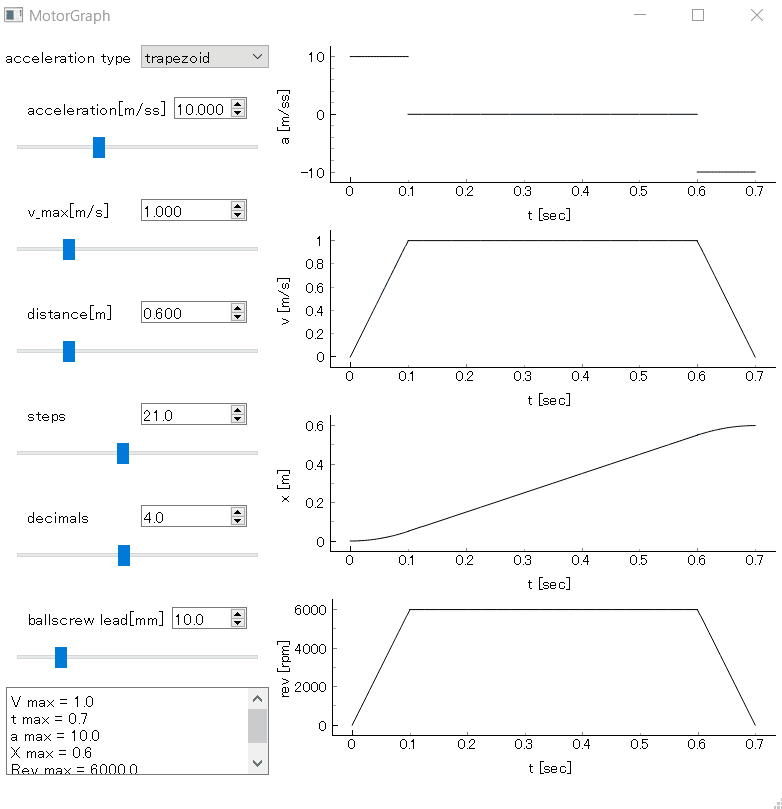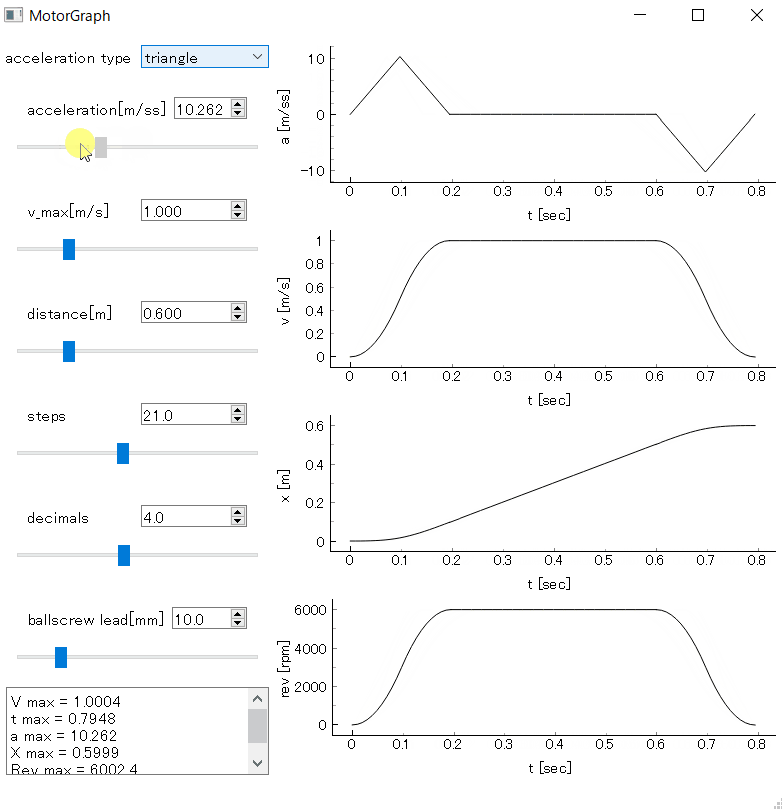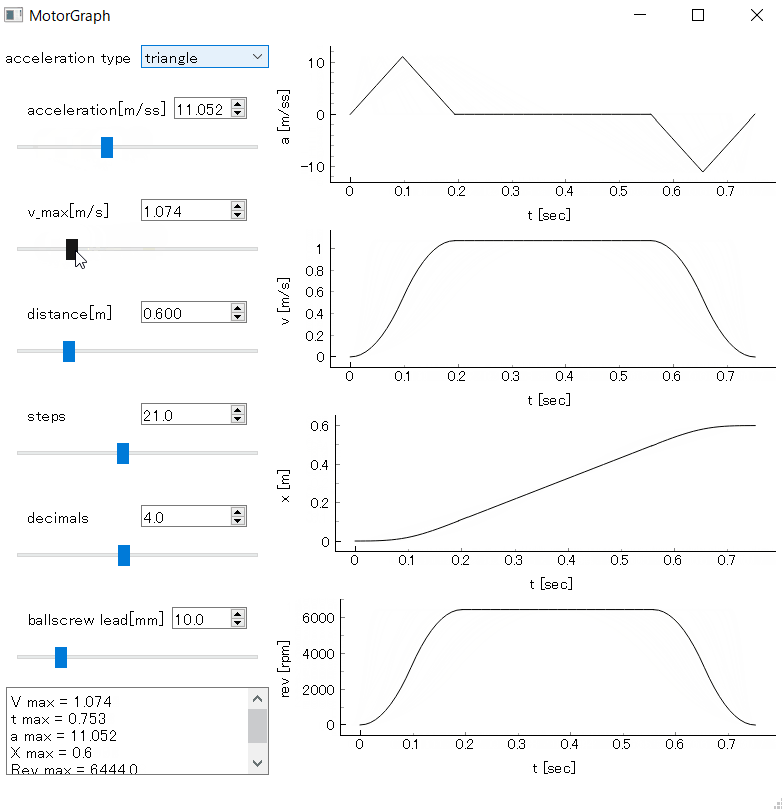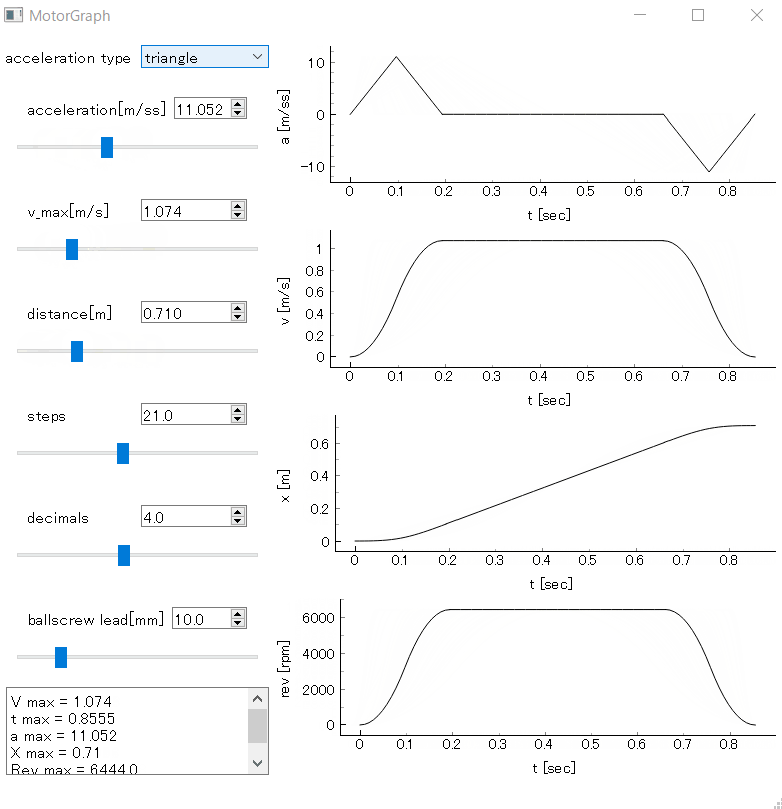
加速パターン

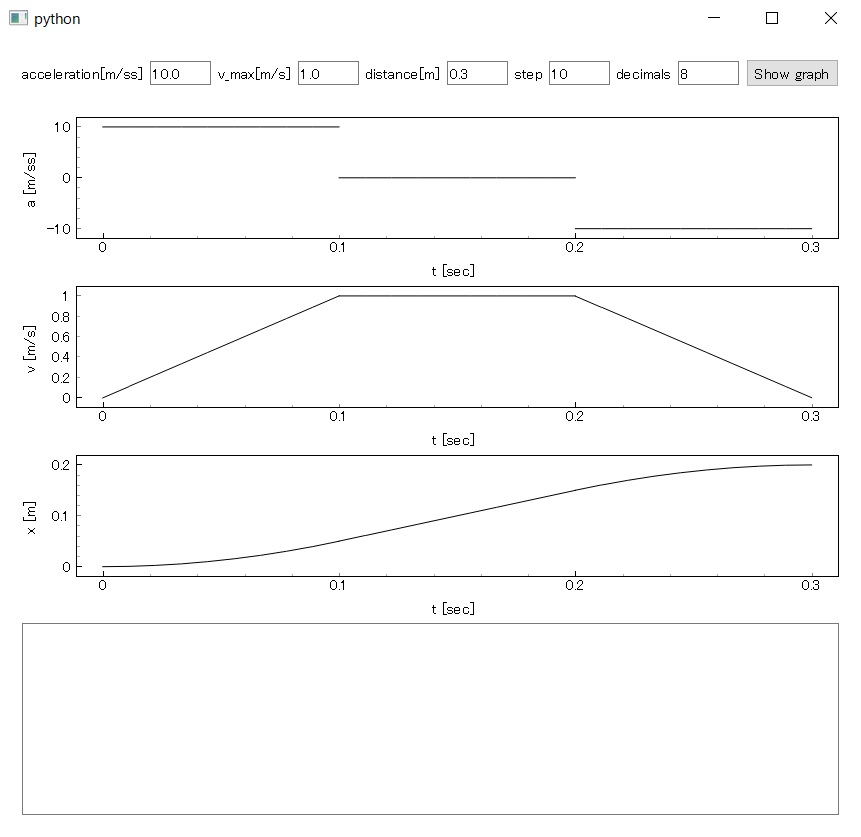
台形駆動のように等加速度運動を行う場合、t=0からいきなり加速度が最大になるため加速時や減速時に衝撃が発生したりします。それを抑えるためには加速度を徐々に変化させるのが常套手段で、S字駆動なんて呼ばれているようです。たぶん加速時の速度がS字カーブの形をしているからそう呼ばれているのでしょう。

加速度を徐々に変化させるパターンはいろいろあるようですが、今回は加速度を直線的に変化させるグラフを描くことにしました。時刻tの時の加速度をa、加速時間をt1とした場合、下記のような条件とします。

t < t1/2のとき、a = a1 * t
t >= t1/2のとき、a = -a1 * t

PythonでS字駆動のグラフ計算

計算はtriangle_accelerated_motionという関数で計算していて、下記のようなコードにしました。

加速度は、上述のa = a1 * tとして計算しています。

速度は、時刻の差分dtと加速度aで微小区間ごとに面積を計算してからnumpy.cumsumで要素番号までの和の配列を計算しています。

距離は、速度と同じ計算をdtとvを使って計算しています。

def triangle_accelerated_motion(v0, t0, t1, x0, acceleration, steps, decimals=4):
    t = np.round( np.linspace(t0, t1, steps), decimals)
    t_shifted = np.insert(t[:-1], 0, t[0])
    dt = t - t_shifted

    split_index = int( len(dt) / 2 )
    if not len(dt) % 2 == 0:
        split_index += 1
    
    # calculate acceleration
    t_splited = t[ : split_index ] - t[0]
    a1 = t_splited * acceleration / t_splited[-1]
    a = np.round( np.concatenate( [ a1, a1[ ::-1 ][ split_index-int( len(dt) / 2 ): ] ] ), decimals)

    # calculate velocity
    a_shifted = np.insert(a[:-1], 0, a[0])
    v = dt * (a + a_shifted) / 2.0
    v = np.round( np.cumsum(v) + v0, decimals)

    # calculate distance
    v_shifted = np.insert(v[:-1], 0, v[0])
    x = dt * (v + v_shifted) / 2.0
    x = np.round( np.cumsum(x) + x0, decimals)

    return t, a, v, x